Amazingly, December’s MathsJam had a non-trivial attendance of six whole people. And not just any people! Puzzling heavyweight David Cushing had yet more Renaissance-era riddles to test us all, and the other regulars were in similarly bamboozling form.

I balanced things out by failing to prepare anything or bringing anything to take notes on and subsequently forgetting most of what the others talked about. So this isn’t going to be a very accurate record of what happened, unless I get some reminders in the comments.

I’m going to start with a rather lengthy deconstruction of a puzzle Matthew Taylor posed:

A “lights out” puzzle

Matthew posted this puzzle on twitter a couple of days before the MathsJam night. That could be considered either a tactical error or a helpful advance-warning because by the time we were all gathered together I had a rather thorough solution and explanation.

The set-up is that we have a $3\times 3$ board, with cells that can be coloured either black or white. We can perform the following three types of move on the board:

1. Change the colour of each cell in one of the rows.
2. Change the colour of each cell in one of the columns.
3. Change the colour of each cell in one of the two diagonals.

Question 1: For any arrangement of the cells, is there a sequence of moves which will leave all the cells the same colour? If not, why not?

First of all, note that if the board is all white, then flipping all three rows will turn the board all black, and vice versa. Hence, an arrangement can be made all black if and only if it can be made all white, so it’s sufficient to show that each arrangement has a sequence of moves which result in the board being all-white.

Now give names to the moves: $R_1$,$R_2$,$R_3$ for the row moves, $C_1$,$C_2$,$C_3$ for the column moves and $D_1$ and $D_2$ for the diagonals.

Any move, applied twice in a row, leaves the board unchanged. Also, the moves all commute – it doesn’t matter what order you do them in.

So each move is either used once or not at all, and the order doesn’t matter.

There are $8$ moves, so there are at most $2^8$ sequences producing different outcomes.

But there are $9$ cells on the board, so $2^9$ possible arrangements, and every arrangement has a different solution sequence.

So straight away, the answer to the question is no: there are some arrangements which can’t be changed to be all the same colour using the moves given.

Question 2: Extend to $N\times N$ grids, with the logical extension of the rules.

An $N\times N$ grid has $N^2$ cells but $2N+2$ moves. By the argument from Question $1$, a grid definitely has unsolvable arrangements when there are more cells than moves, i.e. $N^2>2N+2$.

$N^2=2N+2$ when $N=1+\sqrt{3}\approx 2.7$.

So grids bigger than $3\times 3$ are definitely unsolvable. A $1\times 1$ grid is, of course, already solved by definition.

But what about $2\times 2$?

Question 2(a): How many arrangements really can be “solved” with the given moves?

The answer to this one isn’t necessarily $2^{2N+2}$: if one of the moves can be reproduced using some combination of the other moves, then we don’t have as many degrees of freedom as we thought.

We can immediately get rid of one of the column moves: flip all the rows, so every cell has been changed. Now flip all the columns except one. The flipped columns are back to how they started, and all the cells in the remaining column have changed.

What I’m really trying to do in this question is to find an independent basis (or generating) set for the given moves. You can think about the set of arrangements of a board as a group — as well as representing the colouring of the board, an arrangement can also represent a set of cells to flip. I like this idea because I’m a group theorist.

So when you apply one arrangement to another, each cell in the resulting arrangement is black if and only if it was black in exactly one of the original arrangements. This is functionally the same as the $\mathrm{XOR}$ operation, or addition modulo $2$.

Hence, the set of arrangements that can be solved is the same as the set of arrangements that can be produced using the moves we’re given.

At this point I broke out Python and did a bit of programming. This code is the result. It asks for the size of the board, then it works out how many arrangements can be produced by the given moves and hence how many independent moves there are.

For the $3\times 3$ grid, there are $7$ independent generators, producing $128$ different arrangements, and for the $2\times 2$ grid, there are 3 generators producing $8$ different arrangements. So the $2\times 2$ grid isn’t solvable with the given moves, either!

Question 3: If there are unsolvable arrangements – given any two, can we connect them by a series of moves?

For $3\times 3$ grids, the answer is no, because we’re missing $2$ independent generators. For the $2\times 2$ grid, the answer is yes. Because I’ve spent all afternoon writing up just this puzzle, I’ll leave it up to you to see why and how.

OK, that went on a bit longer than I intended. It’s a good puzzle though, and I used it as an example of applied group theory for a friend doing a third-year algebraic structures course whose lecturer hadn’t seen fit to show him any groups that weren’t ${\mathbb{Z}}^n$ or ${\mathbb{Z}}_n$, or even any applications of those to real problems! He was having trouble understanding what quotient groups are all about so, since we’ve just generated a nice normal subgroup of the group of arrangements of the board, I showed him what you get when you quotient it out: fun times!

On the MathsJam night, I guided the others to this solution with a few hints and nudges, and a grid of pennies representing the board.

Matthew asked where would be a good place to do a PhD in maths, preferably a project on something to with braid groups. It was agreed that funded PhDs are thin on the ground these days, and David (part-time funded) and I (self-funded) weren’t optimistic about the chances of Matthew getting funding at Newcastle, much as we’d like to have him around.

I’m not completely sure who gave this next puzzle, but I think it might have been Matthew again:

A picky-interval game

$A$ and $B$ play a game. They draw out the interval $[0,1]$ and pick a point $x$ inside it. They take turns choosing sub-intervals as follows:

1. each player’s interval has to be contained entirely in the previous player’s interval
2. $A$‘s interval must be exactly $\alpha \in [0,1]$ as big as $B$‘s previous one. Similarly, $B$‘s interval has to be exactly $\beta$ times as big as $A$‘s previous one.

If $B$ picks an interval not containing the point $x$, then $B$ wins. Otherwise, if after infinitely many goes $B$ hasn’t won, then $A$ wins. Player $A$ must have patience in abundance for this game.

I won’t write out a solution because frankly I’m brain-drained from writing up the lights-out puzzle. Anyway, it was rather satisfying to see how the game worked, and David and I did a lot of scribbling:

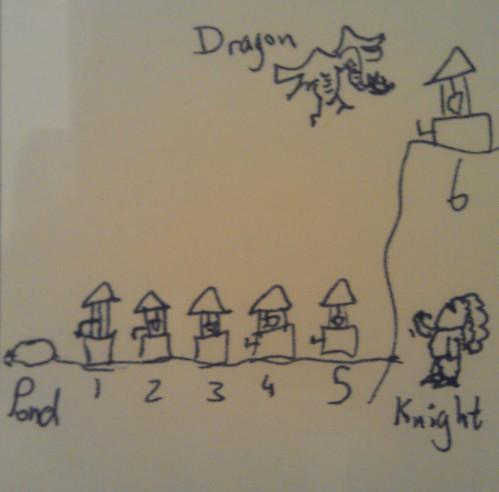
Talking of David, he followed up his excellent princess-on-a-graph puzzle with one about a knight and a dragon:

A knight, a dragon and six poisoned wells.

A knight and a dragon have a fight which ends in a draw. They agree to settle the matter with a battle of wits. They go to a place with a freshwater pond and six poisoned wells. The first five wells are accessible to both the knight and the dragon, but the sixth well is on a high promontory that only the dragon can reach.

Each well is poisoned but the poison can be cancelled out by drinking water from a well with a bigger number. So if somebody drinks from well $1$ and then from well $2$ they will survive, but if they drink from well $2$ and then well $1$, they will still be poisoned and will die the next day.

The dragon and the knight agree to spend the night concocting their strategies, and in the morning they will each go in secret to fetch some water to give to each other.

What happens?

Your ideas, please! I didn’t get the solution without a lot of hints from David.

I also have written down something about a “train puzzle”. I can’t remember what it was. If it was David’s train puzzle, maybe he can talk about it in the comments.

David brought his collection of Rubik’s cube-ish toys:

The pyraminx (the pyramid-shaped one) was the only one I could get my head round. The dodecahedron one was far too hard.

Eamonn brought some puzzling blocks which we were supposed to fit together.

Andrew Lobb pointed out on twitter later on that the one with numbers on isn’t a real die because $4$ and $3$ should be opposite each other.

Dan Woodhouse asked: Assign numbers $1\dots N$ to the vertices of a tree of $N$ vertices. Label the edges with the difference between the numbers at their ends. Can all edges have unique labels?

I had a good sporting go at it until he told me the question is famously open. Oh well.

John asked the following question:

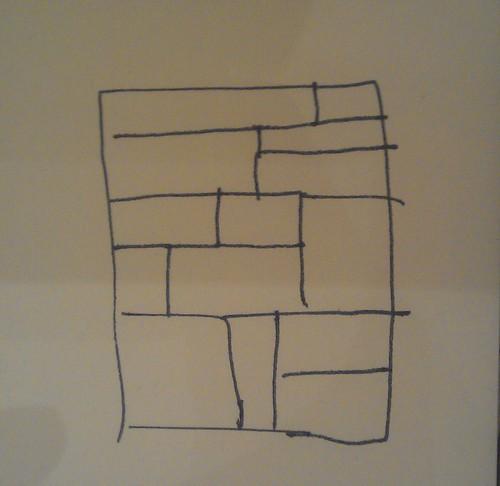
A rectangle is divided up into several smaller rectangles. For each smaller rectangle, either the horizontal or vertical sides have integer length. Is it true that the large rectangle must have sides of integer length?

The answer is yes and John gave three different proofs, all of which I failed to write down. One of them involved integrating $e^{2\pi (x+y)}$ across the whole rectangle.

I have a few other things written down that I can’t fully remember:

• Something about the random number generator in Tetris
• What’s the point in maths?
• Maths is art — I can’t remember if the contention was that maths should be considered alongside the arts subjects instead of the sciences, or whether it was something to do with how elegance or “beauty” are desirable goals in mathematics. Anyway, I definitely remember taking the opportunity to plug my arty maths blog.
• Is there a 3d version of buffon’s needle?
• What fraction of all triangles are acute? This question was discussed by Richard Guy in an essay entitled, “There are three times as many obtuse-angled triangles as acute-angled ones.” No prizes for guessing the answer, but the essay gives five different proofs of the headline value and a few dissenting answers. It’s part of the excellent anthology “Is Mathematics Inevitable?” which I must remember to bring along to MathsJam at some point.

So that was December’s MathsJam. Maybe in January I’ll be a bit better-prepared and take better notes.

By the way, I wrote up our solution to the princess-on-a-graph puzzle last month in a post that has been woefully under-appreciated, judging by the visitor stats. Rectify that, if you would be so kind.