Hey, I haven’t done one of these in absolutely ages! I’ve missed two MathsJams and forgot to write up the other two, so that’s why that’s the case.

September’s MathsJam was very enjoyable. We had some magic tricks, debated the application of game theory to the penal system, almost played a game of rhythmomachy, and of course we solved a few puzzles.

David’s card tricks

David knows a lot of card tricks. He showed us a few, but I think the Magic Circle would do bad things to me if I explained them here. I did record David doing a different, very mathematical, card trick a while ago, so here’s that:

 

Never start a sentence with a proposition

David asked a provocative question: what if, when a prisoner killed another prisoner, they got the murdered prisoner’s sentence taken off their own? What would happen? Would anyone live long enough to serve out their sentence?

A bit of mathematical modelling followed. We assumed that prisoners’ ability to kill each other is directly proportional to the length of their original sentence, and for the sake of simplicity assumed one fight to the death per day, between a randomly chosen prisoner and his target. Because David had a deck of cards out, we used it as a source of random numbers, to give everyone an initial sentence, to pick prisoners and to decide who won fights.

In our simulated prison, Vicky, Ji and Stephen all died; I was released ten days early for killing Vicky; David was released having fought nobody, and John was released after only two days with a bone-chilling seven-day imprisonment credit. We can only hope he doesn’t decide to use it.

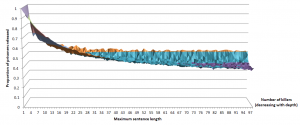
David had actually asked me his question earlier in the day, when we were supposed to be doing proper work, so I wrote a Python script to simulate the game. I’ve assumed that prisoners will choose to fight the opponent with the maximum expected sentence reduction. When sentences range between 1 and 20 days, just over half of all prisoners are released, on average, which I think counts as evidence that our policy is humane. As the range of sentences gets bigger, however, the proportion starts to decrease, as you can see in this chart I made of the results.

The obvious next question to look at is whether length of sentence is correlated with length of stay in prison, either positively or negatively. I’m really not sure what the answer would be.

John’s puzzles

John (or Twitter, I’m not sure) showed us this fun fact:

If you start with a square grid of 25 dots and pick 5 of them, there will always be at least one pair of picked points such that the centre of the line between them lies on a dot.

John also told us the rules of a rather fun guessing game. Player 1 picks a number, and keeps it secret. He then announces a “guess”, which could be any number at all. Player 2 announces a guess, and Player 1 says if it’s closer or further from the secret number than his own. Player 3 then makes a guess, and Player 1 says if it’s better or worse than Player 2’s. I think the aim is for the last player to guess as close as possible to the secret number.

Ji’s puzzles

Ji posed us a couple of nice puzzles. The first began with him emptying his coin purse onto the table.

He then explained: he and anyone who thought they could outsmart him would take turns picking piles to remove any number of coins from. The last person to pick up a coin would be the winner. I think most of us recognised it as Nim straight away, but David played along anyway.

Another game is to take turns picking numbers in the range 1 to 9, with the first person to make 15 the winner. This game is equivalent to noughts and crosses because of the following picture:

Ji ended with a much harder challenge. He claimed that most of the time, when you pick 4 cards from a deck, you can make 24 by combining all of them through addition, subtraction, multiplication or division. We thought about one instance of this a few months ago – can 8,8,3,3 be combined to make 24?

We had a few goes, and found a couple we could make 24 with and a couple we couldn’t. So the jury’s still out. We couldn’t do this set; can you?

When I got home, I wrote a Python script to find solutions, if they exist. It finds the solution for 8,8,3,3 but not for the 4,9,12,13 pictured above, so I reckon it works. It’s a pretty stupid exhaustive search though, so I’m not going to set it off deciding how often sets of cards have solutions.

Back at MathsJam, a few of us started trying to enumerate all the possible expressions on four numbers. We started drawing binary trees, until Ji pulled a pad of paper out of his bag and put an end to the conversation.

More games

I got my homemade Rhythmomachy set out again, but nobody wanted to play after seeing how it sent Eamonn and me mad when we played it for the first time in July.

While I was trying to goad people into playing Rhythmomachy, David started trying to get people interested in the definition of amenability for Banach spaces. This was not a highlight of the evening.

There was a quick game of Tic-Tac-Othello, which I didn’t get a picture of. I made an online version of the game a while ago. The rules are pretty much what you’d expect them to be.

Put a Wieringa roof over your head

I followed Adam Goucher’s instructions for constructing a Wieringa roof from golden rhombi. The Wieringa roof is an aperiodic tiling of the plane with just one kind of tile, but it gets round the fact that nobody knows if one of those exists by allowing the tiles to tilt up and down, producing a corrugated surface whose projection onto the plane looks like the Penrose rhombus tiling.

It turns out I got mine wrong, so it looked a bit odd, but it worked as a hat to protect me from David’s Banach space nonsense. Vicky captured the scene in a photo that definitely didn’t take 90 seconds to pose properly.

I claimed that the secret spy listening posts that are dotted around our countryside use Penrose tilings in their construction to minimise funny diffraction effects as radio waves pass through their shells, but I’ve had a look and I can’t find any evidence to back me up. I’m sure I read it somewhere.

I’ve since had another go at constructing a Wieringa roof, which is going much more successfully so far:

Jokes

We ended the night with a mix of mathematical yo mamma jokes, Gauss facts, and discussion of ways to outwit bookies and lotteries, none of which I can remember.

I had a lot of fun! So much that it prompted me to get back in the habit of writing these recaps. I hope October’s MathsJam is just as good.